MOVING ON TO
THE SMELTERS
As far as is possible to reconstruct in comparison with similar mining sites and factories, the ore, once concentrated in the mines, was transported out of the valley to the talus cone of the Lengerui River, which was approximately 1.5 kilometres from the mines. It is likely that the fahlore was then heated to well above 400 °C in special smelters, allowing for distillation and separation of the thus purified, liquid mercury.
The process applied here was not much different from the process used today for distilling schnapps or other alcohol. The procedure was also recorded in one of the earliest German printed poems, the “Tiroler Landreim”, written in 1558. Mercury was once a valuable element with many different applications. It was not only used to create medicine, but also for amalgamation in gold mines. It was therefore generally considered a great source of income.
Back then, the Gand mines were the only mines in the Tyrol where this specific metal was mined. Even in Schwaz, known as an important silver mining centre due to the huge amounts of fahlore that were extracted here, mercury was not mined until 1923. After all, the mercury content in this region was rather low, rarely amounting to more than 3 to 5 %. It seems as if the Stanzer people have well managed to keep their mercury distilling process a secret.
Once the mercury had been removed, the processed fahlore and chalcopyrite were brought to the territorial silver foundry in Imst. The foundry was originally located at the merging of the Piger and the Malch Rivers. Here, useful metals such as copper and silver were separated from the fahlore by adding lead glance from the nearby Gurgltal lead ore mines, and prepared for further processing.

Fig.: Drawing of the former territorial silver foundry in Imst

Fig.: The talus at the Lengerui River, once a busy mercury distillation site
Traditional
mercury smelter
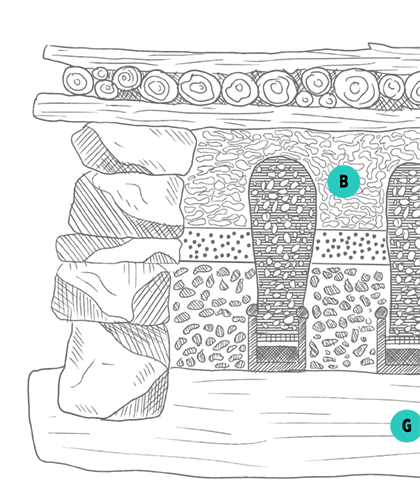

(Illustration © Oliver Kopp)
Scheme for the extraction of silver from fahlore (schwazite) in the Gand mines
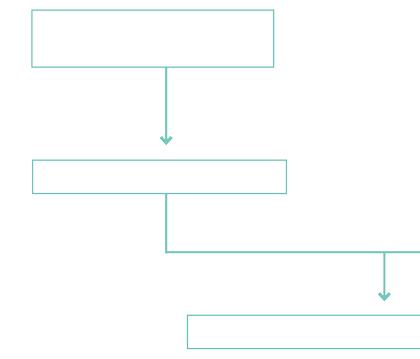

Due to the higher affinity of lead (Pb) compared to silver (Ag), the two metals combined and the copper remained.
Lead and silver are generally heavier than copper and would sink to the bottom of the melter, whereas the copper collected in the upper part of the device.